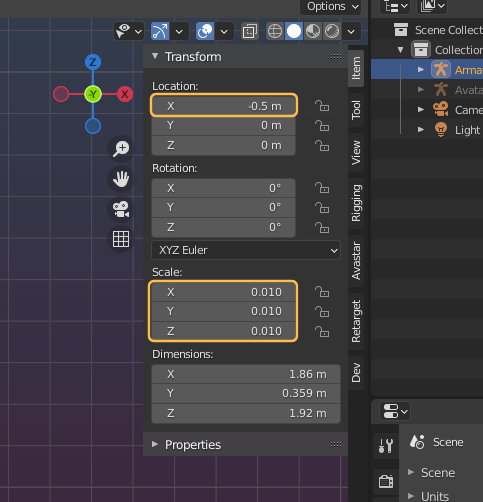
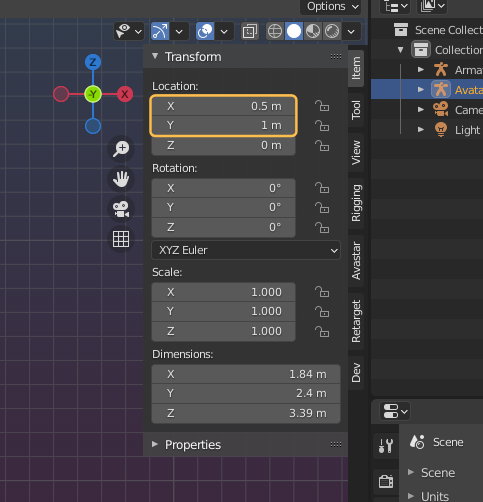
So, lets retarget this thing, its easy enough… You might think. Nope, it is not! At least not for me. I tried to retarget the rig for a few days now and i constantly fail at some subtle differences between the two rigs. Let us see in more detail.
The center bones
We have two challenges when the Mixamo-Hip bone is animated (rotated):
- The rotation axis differs from the axis of the related COG bone in Avastar. This is the first challenge.
- The Avastar COG has its head at the Avastar Pelvis Tail, so we actually would want to retarget the Mixamo Hip to the Avastar Pelvis. But Avastar wants the mapping to go to the COG bone. this is the second challenge
Currently Avastar rejects any attempt to retarget a pose or an animation if the COG bone (from Avastar) is not mapped to a bone on the source rig (Mixamo here). I will look into this issue separately. For now lets assume we must retarget the Mixamo Hip to the Avastar COG and so we need to handle the differing bone orientation somehow.
The arm Bone roll
First of all, the bone roll (rotation around the bone’s local Y axis) can be set arbitrarily. So neither the Mixamo rig is wrong nor the Avastar rig. Now we could handle this easily by modifying the Avastar rig (rolling the arm bones such that the local X axis points upwards. Actually this would work pretty well. But our goal is to provide a retarget tool that does not need any rig to be adjusted to the tool. We want this to go flawless!
Scale and Location
we love challenges… well, we have to handle them at least. Moving objects around in the scene is normal and we should be able to handle this without problems and without actually moving the objects to the center of the scene to avoid issues. Indeed this is the easy part.
But scaling in Object mode is a more serious thing. Normally one would apply scale whenever possible to avoid complications. But when we import objects into the scene then we might end up with scaled and rotated objects. And also in this case we rather want to handle the scale (and rotation) without need to “fix” the retargeting by moving,scaling or rotating the objects.
Let the Quest begin …
So … let us see where we step into issues, how we can fix them and where we will end. Right now when i type these lines i do not yet know if i will be able to reach my goal. But i will try. So lets see where we will end.
So here is where we enter the dungeons. Beware of pythons!
Lets talk about Transformations
You have read this term all over the documentation, you might have an idea what that means, or not… so just in case lets take a brief look at what a transformation is. And no, no mathematics is needed at all, only curiosity and a bit of patience with yourself. So you can safely read on !
So, a Transformation in 3D is a combination of a translation (movement in space), a rotation (rotation in space) and scaling in space. And Space in 3D is always defined by coordinates in 3 dimensions. Ok, this is the theory. lets go into practice and keep it simple and not go into esoteric mathematical theories and such… We would not understand this anyways (most of us including myself).
For us it is enough to look at the Blender scene to see the 3 dimensions, assuming the scene is displayed in Front View:
- X- Dimension going from left to right (using a red axis)
- Y- Dimension going from where you sit in front of the computer to where you look to behind the monitor (using a green axis)
- Z- Dimension going from bottom to top (using a blue axis)
The image at the side is not taken exactly in front view so that you actually can see the Y axis (in green). But i think you know what i mean. Anyways, this is the Blender world coordinate system (as we will use it)
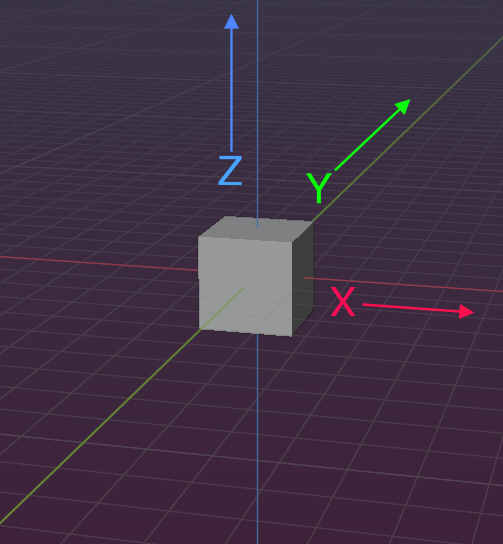
This is NOT front view, – and so you can see the Y axis which would not be visible in front view.
So, now we have defined where (in which space we will live). now lets check out what transformations we can have here. And this comes in very naturally:
- You can move an object along the X/Y/Z axis
- You can rotate an Object around the X/Y/X axis
- And you can Scale an Object along the X/Y/Z axis
And as stated before: A transformation is a movement plus a rotation plus a scaling along X/Y/Z:
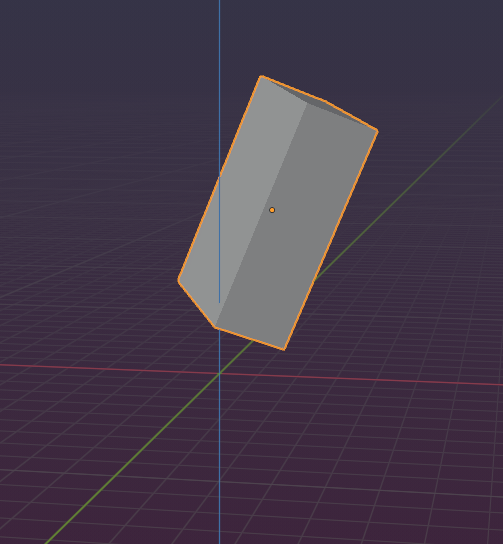
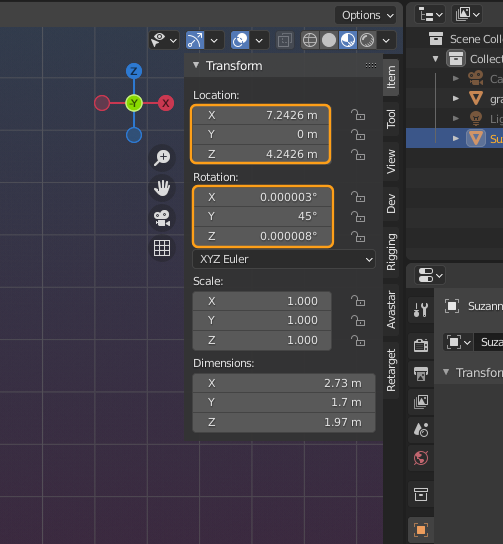
This cube is moved, rotated and scaled
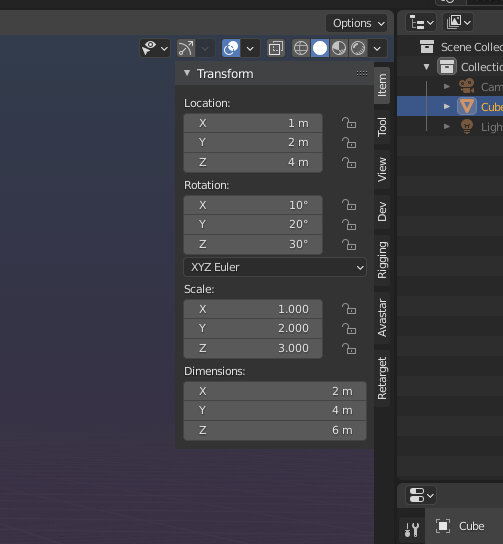
You find the exact values (9 numbers) in the Transform panel of Blender (item tab)
So in principle we can describe a transformation by 9 numbers, 3 for each axis and from those one for movement along the axis, one for rotation along the axis and one for scaling along the axis. easy…
… easy as long we look only at one object
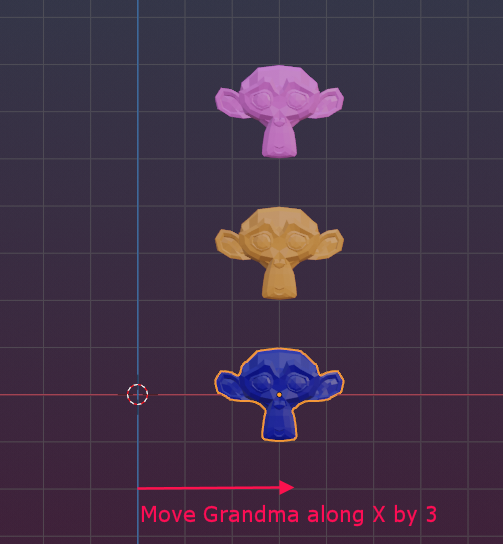
Things are quickly running out of control when you have to work with an object hierarchy. For example look here: Those are:
- Grandma at location (0,0,0)
- Mama at location (0,0,3)
- Suzanne at location (0,0,6)
I have added a parent hierarchy to those three objects, So Mama is child of Grandma and daughter is child of Mama… well… In blender that means: When Grandma gets a transformation, then Mama and Suzanne inherit that and also move …
Lets make a simple test. Move Grandma sideways on the X-axis by 3 blender units, so her new locations in the scene will be (3,0,0). But since Mama and Daughter are child and grandchild of Grandma they both inherit the movement, thus:
- Grandma:(3,0,0)
- Mama: (3,0,3)
- Suzanne: (3,0,6)
Easy again, we can see that!
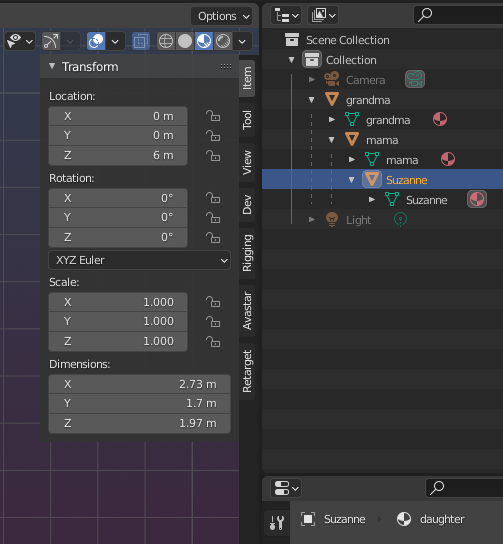
well, lets take a look …
at the transformation data of Suzanne.
we see the location is still at (0,0,6) but we clearly see that Suzanne is shifted by 3 in X as well! So we expect to see (3,0,6) here! Blender is broken… You might think…
But no, it is not …
What you see here is not the location in the scene. But the location relative to the Grandma! Or simple again …:
The location of Suzanne in the scene is actually the location of Grandma in the scene (3,0,0) plus the location of Suzanne relative to Grandma (0,0,6):
(3,0,0) + (0,0,6) = (3,0,6)
Now it makes sense again. OK, but since we are brave people, we now turn over to rotating Grandma by 45 degree…
So how do we get the exact location of Suzanne in the scene? Blender does not tell us, so we have to do something now …
Lets call the pythons ?
No wait, we have an option! We can break the parenting of Suzanne. then the Object should tell us where it is…
Object -> Parent -> Clear Parent
Aha!!! What Blender told us all the time is the location of the object at the time when it was parented. So when unparenting it, then it snaps back to where it was originally parented. this sounds familiar? You encountered this issue ? probably yes, probably more than once and probably you thought it was a bug. No, it is intended behavior!
ok, the trick is:
Object -> Parent -> Clear and keep Transformation
The function name actually tells it all. And Suzanne stays at its location, finally the Transformation data in the Transform panel tells us where she is in the scene…
So we are done, the world is shiny and the birds are tweeting and all is well in Blender world…. scratchhhh….
Until we remember what our goal is, namely retargeting a rig. Wait what? is this related to what we just have seen ? oh my god…
Now we need the Pythons … right ?
no, we first need to talk about a concept, that is frightening stuff for most of the people in the world, and i believe that it has become popular only from a movie! So, prepare to flee! or keep brave, it can be fun to some extend … I am talking about …
The most important and least understood thingy in 3D aka: The Transf…
Ok, full stop, lets first step back to first class in school, because there you find all you need for survival (almost)… You know these symbols…: + – * / that is a well known set of operations which can be used to calculate simple numbers like 1+1 = 2 for example, or 20*2 = 40 … ok, ok, simple enough! Lets keep with the “*” for a minute and see what rules we have for “multiplication”.
Concept building… (i love it)
Just so you know where this is going: I explain what multiplication does with real numbers in a somewhat more general way than most of you probably have seen it before. So: Multiply is an operation on numbers with a few interesting properties you all know about but you probably never thought of being anywhere important. But the concepts work pretty well also for what comes next …
- First thing is: the Multiply operation always works on 2 numbers (2*4, 3*5, …)
- Then: Whatever comes out as a result of a Multiply, is still a number (pff trivial)
- There is a neutral number (‘1’ in our case), so when you Multiply any number by the neutral number,
then the result is the number itself: 3*1 = 3 , 5*1=5, … - For (almost) any number there is a an inverse number such that the result of Multiplying the two numbers
is always the neutral number’1′: 4*0.25 = 1 or 20*0.05 = 1 … - and then there is the null… the bad guy in the universe. I am not sure if i like it … And the inverse of null is infinity… well, actually i believe the inverse element of null is not even defined. So, null multiplied by its inverse does not give us anything, not even a ‘1’ as one might expect… null is really a bad guy isn’t it ? Lets ignore it and just keep aware it is lingering somewhere in the dark and once in a while it lets crash Blender …
You get this until here ? so lets go over it once more in more general terms (i replace ‘number’ by ‘element’):
- We have an operation (multiply) with the commonly used symbol “*”
- Whichever 2 elements we multiply, the result is always an element as well
- We have a neutral element (1)
- Each element (E) has an inverse element (I) such that E*I=1 (except for the null)
- There is a bad guy in the universe, aka the null element
Let it sink in, put it aside, we get back to this soon. Again: take this with you as a cheat sheet. It is not too important, but it is good to have those rules in mind, we need them soon. So second try…
The most important thingy in 3D aka: The Transformation Matrix
Think of it as a mathematical unit with a bit of inner structure, but not very different from simple numbers. First of all lets keep in 3D so we talk about 2 types of matrices: 3×3 matrix and 4×4 matrix.
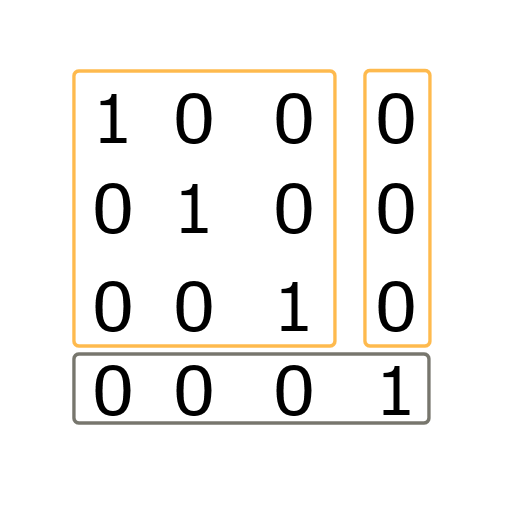
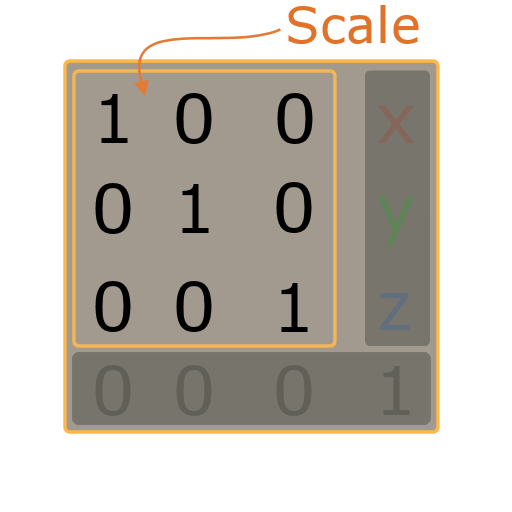
Basically a matrix is a list of n rows with each row being a list of n numbers (in our context). A simple example of a 4×4 matrix is shown in the image aside. A box with 16 numbers this is (says Yoda), nothing more, nothing less!
Ok, now you are completely lost? Forget everything about how on earth all of this might possibly work, it is not super important. What is important though is what a matrix stands for (what is the meaning of Matrix?) and how we can work with matrices almost as if they where simple numbers! For now just accept that a matrix is a set of 3 (or 4) rows where each row contains 3 (or 4) numbers. not more, not less, 16 simple numbers!!!
So, now about the meaning…
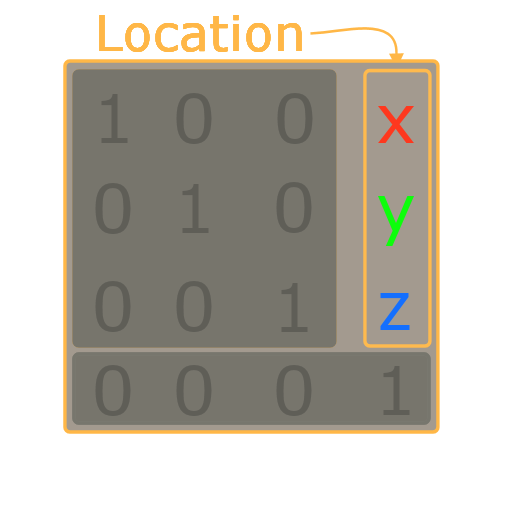
Think of it as a bag that contains three ingredients:
The location is always placed into first 3 places of the right most column. the data are the values for the x,y,z axes
This is also called the Location Vector.
Hint: When all 3 location elements are 0 then this is the neutral element regarding location changes (translation).
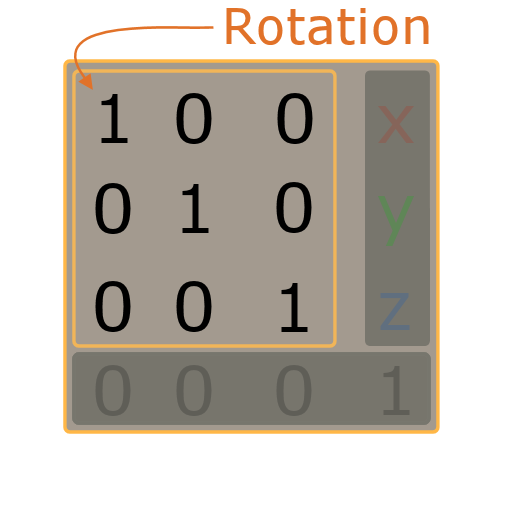
The rotation is placed into the top left corner. it is always formed as a 3×3 Rotation matrix. How the rotation is stored into the matrix is not in our scope, but it is there, i swear.
The scale is placed inside the Rotation matrix. And again, we won’t say how the scale is stored, but it is there.
Hint: If the matrix rotation is 0 (no rotation component) then the scale is actually located in the diagonal that is marked in the image with the numbers ‘1’ with:
- x-scale at the top left corner
- y-scale in the middle of the 3×3 matrix
- z-scale in the bottom right corner of the 3×3 matrix
BTW: this 3×3 matrix has no rotation and all its scale elements are 1. Think of it: This represents the neutral element regarding rotation and scale.
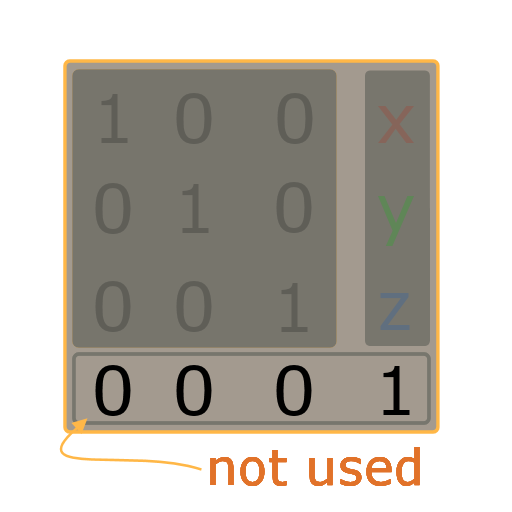
There is still the bottom row in the Matrix. This row always contains the numbers (0,0,0,1) and it does not contain any transformation related data.
You may just think of this row to be there only to make the thing a 4×4 Matrix.
phew… well.. was it really so complicated until here? just allow yourself to be blind for how this will be usable but just keep in mind what the meaning of the thingy is.
And BTW … By now you even can figure out what the matrix in the image aside means when looking back on what i wrote above:
- location: 0,0,0
- Scale: 1,1,1
- Rotation: None
Yeah… and this is …
The Neutral Element of the Matrix Universe, aka the Identity Matrix, now we are good to go one step further…